
₪ 1. RÉSEAUX GÉODÉSIQUES
Un réseau de points connus en planimétrie est nécessaire pour effectuer la majorité des travaux de topographie. Ce n’est pas indispensable dans le cas où le travail sera effectué en repère local (petits chantiers ou chantiers isolés). L’Institut Géographique National (IGN) a donc implanté en France un réseau de points dits « géodésiques » (voir la carte figure 2.39. Sur laquelle on distingue la triangulation du 1er ordre achevée en 1958).
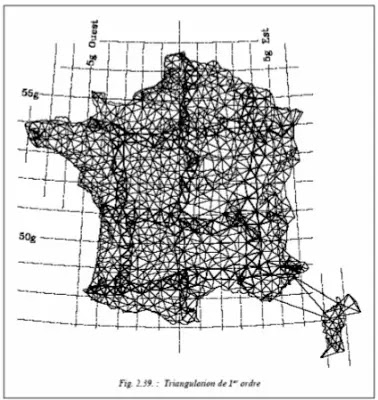

La détermination des points géodésiques s’est faite par la méthode de triangulation, qui consiste à mesurer les angles et quelques côtés des triangles accolés dont les sommets sont les points géodésiques. La résolution de ces triangles donne les positions relatives des sommets. Le problème étant d’implanter sur le territoire un ensemble plus ou moins dense de points, on procède par triangulations emboîtées ou ordres géodésiques hiérarchisés, respectant ainsi le principe « aller de l’ensemble au détail ». Cela permet d’assurer une précision homogène entre les différents ordres de réseaux.
₪ 1.1 Historique de triangulation
Le but initial de la triangulation consiste à connaître la forme et les dimensions de l’ellipsoïde terrestre,
❏ D’ossature à la carte de France à petite échelle ;
❏ De base à l’établissement des plans cadastraux à moyenne échelle ;
❏ De canevas pour les plans à grande échelle établis pour les grands travaux
❏ Aux besoins militaires. L’évolution a imposé des plans à des échelles de plus en plus grandes et donc des canevas de plus en plus précis :
❏ En 1792, Méchain (1744 –1804) et Delambre (1749–1822) ont mesuré l’arc de meridienne Barcelone de Dunkerque en vue de la détermination de l’unité de longueur. Cette chaîne méridienne sur mesure fut le point de départ de la triangulation qui a servi de base à la carte d’état-major au 1/80 000 ;
❏ En 1873 débutent les travaux de la Nouvelle Triangulation Française (NTF). Mais il n’a pas été possible d’utiliser les points de l’ancienne car la précision s’est avérée insuffisante, de nombreux points étant des pins, hêtres, rochers gravés, tours, d’une conservation douteuse. On a donc cherché à constituer plusieurs ordres de triangulation avec des visées suffisamment nombreuses situées dans les différents quadrants et de longueur homogène. Les points ont été matérialisés par des bornes d’importance plus ou moins grande selon l’ordre ;
❏ En 1991, année de la dernière campagne de géodésie classique de l’IGN, la NTF a été déclarée achevée : elle s’était régulièrement enrichie au fil des années par densification à partir du réseau de 1er ordre jusqu’à atteindre une densité d’un point pour 9 km2 environ avec le 4e ordre. Ses 70 000 sites géodésiques (sans compter les points de 5e ordre) sont uniformément répartis sur le territoire national avec une précision relative moyenne de l’ordre de 10–5 (c’est-à-dire plusieurs centimètres au mieux par rapport au point le plus proche).
❏ Le nouveau système géodésique RGF 93 est en préparation.
₪ 1.2. La nouvelle triangulation française (NTF)
Un siècle aura donc été nécessaire à l’élaboration de ce réseau (de 1873 à 1991). Il est constitué :
❏ D’un point fixe, le point géodésique fondamental, qui est la croix du dôme du Panthéon à Paris dont on a déterminé avec le maximum de précision les coordonnées géographiques déduites de l’observatoire de Paris de coordonnées géographiques :
❙= 0,0106 93 gon ; = 54,273 618 gon ❙
On y a aussi mesuré l’azimut astronomique du côté de départ de la triangulation. En ce point, la normale à l’ellipsoïde et la verticale qui est la normale au géoïde sont confondues ; l’ellipsoïde Clarke 80 y est tangent au géoïde. L’altitude et la hauteur ellipsoïdale sont égales.
❏ De 15 bases géodésiques d’une dizaine de km mesurées au fil Invar (précision 1 cm) réparties tous les 250 à 300 km ; elles sont destinées à réajuster les dimensions des triangles ;
❏ Des stations de Laplace, servant à réorienter les côtés des triangles à chaque base ; par des visées astronomiques, on détermine en ces points l’azimut d’un côté du triangle.
₪ 1.2.1. Réseau de premier ordre
Il comprend les éléments suivants :
❏ Le 1er ordre de chaîne : trois chaînes méridiennes ont été établies (celle de Bordeaux, celle de Lyon et celle de France qui passe par Paris) et trois chaînes parallèles, de Paris, Lyon et Toulouse (voir carte figure 2.39.). Ce sont des chaînes de triangles de 30 à 60 km de côtés et, dans chaque quadrilatère formé par deux triangles accolés, on détermine l’orientation de la deuxième diagonale ; ainsi, les mesures sont en surnombre (huit angles par quadrilatère). Les angles sont mesurés avec seize réitérations. Le 1er ordre de chaîne a été calculé sur l’ellipsoïde en coordonnées géographiques par fractions insérées entre deux bases (fig. 2.41.).
❏ Le 1er ordre complémentaire, constitué par les points de 1er ordre compris dans les mailles formées par les chaînes méridiennes et parallèles. Il est calculé dans le plan de projection en coordonnées rectangulaires par blocs insérés entre les points précédemment déterminés. Les angles ont été mesurés au théodolite T3 (Leica) avec seize réitérations ; pour les réduire au plan de projection, on applique la correction de d
Les triangulations de 1er ordre sont orientées par des azimuts astronomiques (stations de Laplace) et mises à l’échelle par des mesures de longueur. Les compensations ont été faites par la méthode des moindres carrés (calculs en bloc).
Il y a environ 860 points, formant 1 700 triangles de 30 à 40 km de côtés ; 5 000 directions ont été observées. La précision moyenne d’une observation est de 2 dmgon, soit environ 13 cm à 40 km. En règle générale, on considère que les points de 1er ordre sont déterminés à 10 cm près, soit une précision relative d’environ 1/400 000 sur les côtés.
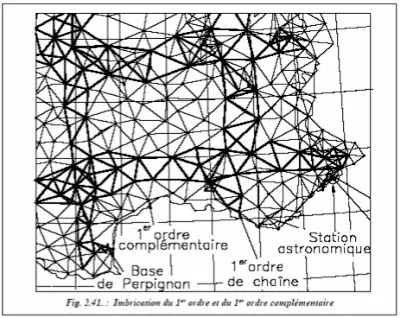

Son manque de précision tient plus à la qualité non optimale des calculs : en effet le réseau s’appuie sur un calcul de la méridienne de France datant des années 1930 et sur le calcul du 1er ordre terminé vers les années soixante ; il n’était pas possible à cette époque de traiter la totalité des observations de 1er ordre, alors qu’aujourd’hui il suffit de quelques minutes pour traiter les observations des 6 200 points de 1er et 2e ordre de la NTF grâce à l’informatique.
₪ 1.2.2. Réseaux de détail
Pour atteindre la densité requise tout en maintenant la précision relative du 1er ordre, on établit successivement les réseaux emboîtés suivants (fig. 2.42.) :
❏ Triangles de 2e ordre dont les côtés mesurent 12 à 15 km environ : appuyés sur les points du 1er ordre, ils sont calculés par blocs d’une dizaine de points ;
❏ Triangles de 3e ordre dont les côtés mesurent 8 à 12 km environ : appuyés sur les ordres supérieurs, ils sont calculés comme ceux du 2e ordre ;
❏ Triangles de 4e ordre dont les côtés mesurent 3 à 4 km environ : ces points sont généralement calculés en points isolés à partir de visées de 3 à 6 km.
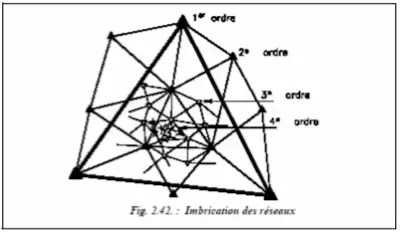

Dans chaque triangle d’un ordre donné, il y a environ trois points de l’ordre immédiatement inférieur.
Les angles ont été mesurés au théodolite T3 (Wild) avec huit réitérations pour le 2e ordre et au théodolite T2 (Wild) avec quatre réitérations pour les 3e et 4e ordres. Pour les 2e et 3e ordres, les visées ont généralement été observées dans les deux sens, ce qui permet de fermer les triangles et de déceler ainsi les anomalies. Les compensations sont faites par la méthode des moindres carrés par groupe de deux à dix points.
₪ 1.2.3. Réseau de cinquième ordre ou triangulation complémentaire
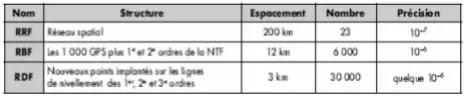
La densité du 4e ordre est insuffisante pour rattacher directement les cheminements topographiques. Dans certaines zones, on a donc établi une triangulation complémentaire. Chaque détermination a été faite en général par relèvement avec deux réitérations au théodolite T2. Le Tableau suivant récapitule les ordres de triangulation.


₪ 1.2.4. Matérialisation des points géodésiques
₪ 1.2.4.1. Borne géodésique
Une borne est un bloc solide en granit dont la partie émergeant du sol est un cube de 15 cm d’arête. La face supérieure horizontale porte une croix gravée matérialisant le repère supérieur. La borne repose sur une dalle. La borne et la dalle sont prises dans un bloc de béton. Sous celui-ci, séparé de lui par une couche de terre meuble, est coulé un bloc de béton dans lequel est ménagé un orifice circulaire au fond duquel se trouve un repère métallique inférieur recouvert de charbon de bois. La borne est placée de sorte que le repère supérieur et le repère inférieur soient à l’aplomb l’un de l’autre. La profondeur de l’ensemble est environ 0,80 m, et le poids du bloc de granit est de l’ordre d’une tonne.
₪ 1.2.4.2. Mire géodésique
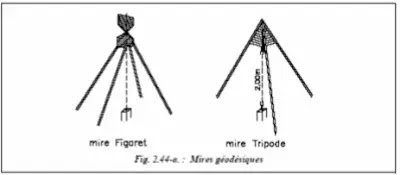
C’est un ensemble de panneaux de forme géométrique, en bois ou en métal, ayant un axe vertical centré au-dessus d’une borne ou d’un rivet (en montagne). Les mires géodésiques permettent l’observation éloignée de ces points. Les mires métalliques sont démontables. La hauteur des panneaux et la disposition des montants permettent de mettre un appareil en station sous la mire (fig. 2.44-a.).

₪ 1.2.4.3. Signal
Le signal est une construction ayant un axe de symétrie vertical situé au-dessus d’un repère et permettant l’observation éloignée de celui-ci. Le signal est en général géodésique : cheminée, pylône etc. ; il est souvent pérenne alors que les mires géodésiques sont provisoires. Par extension est englobé sous ce terme toute construction pouvant être observée : cheminées, pylônes, mires géodésiques, balises.


₪ 1.2.5. Répertoires de l.IGN
L’Institut géographique national publie pour chaque feuille au 1/50 000 un répertoire comprenant :
❏ Une réduction de cette feuille sur format A4 avec l’emplacement de chaque point géodésique et son numéro d’ordre dans la feuille ;
❏ La fiche signalétique de chaque point : c’est un document d’archives et de diffusion qui contient :
❏ Des renseignements d’ordre administratif : nom du point, nom et numéro de la feuille au 1/50 000, département, numéro de l’arrêté de servitude, renseignements cadastraux ;
❏ Des renseignements d’ordre technique : désignation du type de borne et des repères auxiliaires, indication d’un point naturel connu pouvant servir d’orientation sur un point inconnu, situation topographique, plan des environs, croquis de repérage, nature et date de la mission et les coordonnées planimétriques X, Y (E, N) centimétriques.
L’altitude H est déterminée par nivellement indirect géodésique avec une précision décimétrique.
Les fiches signalétiques sont stockées sur microfiches X, Y, Z vendues par l’IGN (une microfiche contient 60 points). Depuis fin 1997, tous les points du RBF et de la NTF de 30 départements sont accessibles par minitel (08 36 29 01 29 ; 9,21F par minute au 1/1/98)


₪ 1.3. Le nouveau réseau géodésique français
De nombreux points sont difficilement accessibles, souvent inexploitables car non entretenus, et leur localisation n’est pas toujours celle souhaitée par l’utilisateur. La précision de la NTF est estimée à 10–5 en relatif (1 cm par km) ; elle est insuffisante compte tenu des techniques modernes de positionnement, en particulier le positionnement satellitaire par GPS qui donne une précision relative de 10–6 voire de 10–7 à 10–8.
Déjà le niveau de précision de la NTF avait été mis en question par ses utilisateurs dès l’apparition des distance mètres optoélectroniques précis dans les années 70.
Un réseau géodésique moderne doit donc être constitué de points :
❏ Accessibles,
❏ D’une précision suffisante,
❏ Exploitables par l’utilisateur en fonction des moyens dont il dispose : théodolites, distance mètres, récepteurs GPS.
Donc la NTF ne répond plus aux besoins des utilisateurs ; de plus, il est maintenant nécessaire de disposer d’un système de référence au niveau européen. Il a donc été envisagé :
❏ De mettre en place un nouveau canevas national appelé Réseau Géodésique Français (RGF), qui matérialisera un nouveau système de référence nommé RGF 93, tridimensionnel et géocentrique, constituant une réalisation précise du système WGS 84 ;
Il est organisé en trois niveaux principaux : le RRF, le RBF et le RDF c’est-à-dire réseau respectivement de référence, de base et de détails français ;
❏ De maintenir ce réseau par des observations GPS. Le but est d’obtenir un réseau dont les coordonnées tridimensionnelles dans un système de référence géocentrique sont connues avec une précision de qualité spatiale. La NTF continuera d’exister au sein du RGF, qui intégrera la quasi-totalité des anciens points géodésiques (de cinq ordres).
₪ 1.3.1. Définition du réseau géodésique français (RGF 93)
₪ 1.3.1.1. Système de référence
Ce système géodésique, appelé Réseau Géodésique Français 1993 (RGF 93) est spatial, tridimensionnel et géocentrique ; il sert de base à la création d’un réseau géodésique moderne français par densification des points européens du réseau mondial associé ETRS 89 (Européen Terrestriel Reference System 1989). Le système ETRS 89 est défini à partir de l’ITRS (International Terrestriel Reference System) et coïncide avec lui à l’époque 1989. L’ITRS, système mondial de référence terrestre de l’IERS (International Earth Rotation Service), prend en compte les déformations de la croûte terrestre et en particulier celles dues à la tectonique des plaques ; il est matérialisé par un réseau mondial d’environ 200 points obtenus avec des précisions centimétriques par des techniques spatiales très précises comme VLBI, Laser ou GPS très précis. Ce système évolue et ses différentes réalisations sont appelées ITRF nn, où nn signifie l’année de la réalisation, ITRF 96 étant la plus récente.
De même, l’ETRF nn, réalisation de l’ETRS utilise des points ITRF nn européens et des points de densification par GPS. L’ETRS est rattaché à la partie stable de la plaque Eurasie ; il présente l’avantage de rendre négligeables presque partout en Europe les déplacements des stations dus à la tectonique des plaques. Ce système est de type tridimensionnel, mais l’altitude est fournie dans le système altimétrique actuellement en vigueur (IGN 69).
La technique d’observation des points du RGF 93 est celle de la mesure satellitaire gps triangulation assurant une cohérence de niveau centimétrique aux coordonnées publiées des différents points. Les coordonnées sont fournies, soit sous forme de longitude l, latitude j et hauteur ellipsoïdale h sur l’ellipsoïde IAGRS 80, soit sous forme bidimensionnelle, selon la projection Lambert 93.
₪ 1.3.1.2. Structure hiérarchique
En France, le réseau Géodésique Français (RGF) matérialise ce nouveau système de référence RGF 93. Ce réseau est structuré en trois parties (fig. 2.45.) :
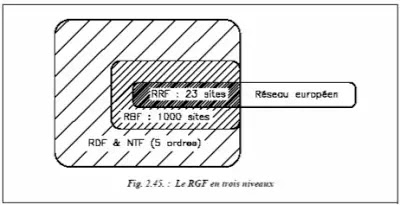

₪ Le Réseau de Référence Français (RRF) : c’est la partie française du réseau européen dont la première réalisation date de 1989. C’est aussi le premier niveau hiérarchique du RGF, constitué de 23 sites répartis sur l’ensemble de la France métropolitaine ;
₪ Le Réseau de Base Français (RBF) : il comprend environ 6 000 points (1 009 sites observés par GPS et nouvelle compensation des observations de 1er et 2e ordre de la NTF)

Le Réseau de Détails Français (RDF) : c’est par densification du RBF que sera réalisé le réseau de détail (environ 80 000 points). Dans un premier temps, le RDF sera constitué des points de la NTF. Ci-dessous est donné un tableau récapitulatif des différents réseaux :
₪ 1.3.2. Réalisation du réseau général français (RGF)
La réalisation d'un système de référence est l'ensemble des repères qui le matérialisent.
₪ 1.3.2.1. Établissement du réseau RRF
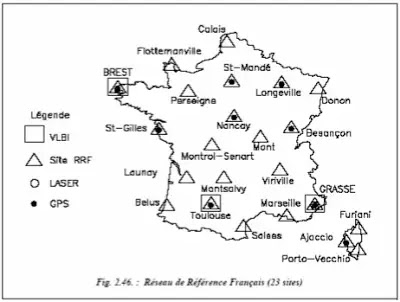
Le Réseau de Référence Français (RRF) possède 23 points (fig. 2.46.). Il se caractérise comme suit :
❏ Une précision relative de 0,1 ppm (10–7, soit 0,1 mm/km) ; la précision entre deux sites du RRF est centimétrique, et sa cohérence vis-à-vis du réseau européen est également centimétrique ;
❏ Une campagne Very Long Base Interférométrie (VLBI) ; c’est la technique la plus précise de positionnement ; elle fait appel à des mesures astronomiques. Cette campagne a permis de déterminer six points en Europe dont deux en France : Brest et Grasse. Les coordonnées de ces points sont connues avec une précision relative de 0,01 ppm (1 cm sur 1 000 km ; remarquons qu’à ce niveau de précision, la dérive des continents n’est plus négligeable !) ;
❏ Ces points ont servi d’appui à 93 points observés la même année par une campagne GPS, dont six nouveaux points en France : Saint-Mandé, Longeville, Nançay, Saint- Gilles et Toulouse. Ils sont en quelque sorte le réseau de base du RRF ;
❏ Puis trois campagnes pour les 15 autres sites représentant le réseau complémentaire du RRF.

Le RRF participant à l’élaboration des réseaux européens et intercontinentaux, il permet au RGF d’être cohérent avec les références mondiales.
₪ 1.3.2.2. Établissement du réseau de base français (RBF)
Le Réseau de Base Français (RBF) possède 1 009 points (y compris le réseau RRF). Il est le deuxième niveau hiérarchique du RGF et comprend un millier de sites géodésiques uniformément répartis tous les 25 km en moyenne ; leurs coordonnées sont déterminées à partir de celles du RRF par des méthodes gps triangulation permettant de conserver la précision centimétrique (précision relative » 4. 10–7).
Il est plus particulièrement destiné aux utilisateurs de GPS qui pourront, grâce au RBF, se positionner au centimètre près, partout en France, en utilisant des méthodes GPS monofréquence, ou GPS statique-rapide. 63 % des sites sont entièrement nouveaux et 37 % sont des sites anciens NTF repris et complétés. Ces points sont déjà disponibles sous forme de fiches imprimées (comme les points géodésiques de la NTF).
Les principales caractéristiques du RBF sont les suivantes :
❏ La présence d’au moins deux repères par site, de définition millimétrique ;
❏ L’accessibilité à tout véhicule, par tout temps (à moins de 30 m) ;
❏ Son adaptabilité à tout type d’exploitation, aussi bien traditionnelle que par GPS : il y a possibilité de mise en station et absence de masque en direction du Sud ;
❏ Des coordonnées de précision centimétrique dans le nouveau système RGF 93 ;
❏ Les coordonnées NTF (Lambert) et les altitudes NGF seront disponibles.
La plupart de ces sites étant rattachés directement à des points NTF et à des repères NPF, le RBF fournira de nombreux points dans les différents systèmes (NTF et WGS 84). L’étude des différents jeux de coordonnées ainsi disponibles permettra à l’IGN de définir des procédés de transformation permettant de passer aisément d’un système géodésique à l’autre ; ces paramètres de transformation seront vraisemblablement fournis pour chaque feuille au 1/25 000.
₪ 1.3.2.3. Établissement du réseau de détails français (RDF)
Le Réseau de Détails Français (RDF) sera constitué d’un nouveau canevas de points le long des 75 000 km lignes des 1er, 2e et 3e ordre du NPF (Nivellement de Précision de la France. Les caractéristiques générales sont les suivantes :
❏ Les points seront situés le long des itinéraires du NPF : un point RDF tous les trois kilomètres soit 25 000 points et 5 000 points complémentaires choisis entre les lignes des trois ordres du NPF ;
❏ Coordonnées RGF 93 déterminées par GPS (statique rapide) en s’appuyant sur le RBF ;
❏ Déterminations altimétriques su centimétriques (altitudes normales).
₪ 1.3.3. Matérialisation
Pour garantir une précision relative de 1 ppm (1 mm par km), la définition géométrique des points doit être millimétrique.
Pour le RRF, le type de matérialisation retenu est une borne de 1 m3 de béton implanté au ras du sol, doublée par une borne de 0,5 m ´ 0,5 m ´ 0,8 m. Les deux bornes ont au centre de leur face supérieure un repère en laiton du type IGN.
❏ Pour le RBF, il faut distinguer :


a) 37 % des sites appartenant à la NTF : on retrouve la borne en granit gravée IGN : au centre de la croix gravée au sommet de la borne est rajouté un repère en laiton permettant un centrage de précision millimétrique et une meilleure définition altimétrique. D’autre part, généralement sur le radier est apposée une plaque identificatrice en bronze (ci-contre) signalant que ce point géodésique a bien été à nouveau déterminé dans le nouveau système RGF.
b) 63 % des sites entièrement nouveaux ; deux types de matérialisation ont été conçus :
❏ Une borne dite « borne RBF lourde », constituée d’un bloc de béton cylindrique de 50 cm de diamètre pour un mètre de profondeur. La partie visible est un radier carré à ras du sol de 60 cm de côté, muni d’un repère hémisphérique en laiton en son centre, et signalé par la plaque identificatrice de l’IGN (ci-dessus) ;
❏ Une borne préfabriquée en polyester-béton (béton armé de fibres) dite « borne RGF légère » ancrée au sol ; la tête de section carrée de 15 cm de côté et de couleur jaune affleure ; un repère hémisphérique est scellé en son centre et la plaque identificatrice est remplacée par les trois lettres IGN gravées sur une plaque en aluminium.
₪ 1.3.4 Système RGF 93
Une nouvelle projection plane a été choisie pour exprimer les coordonnées RGF 93 ; bien que de type Lambert, ses paramètres n’ont rien de commun avec le Lambert associé au système NTF. C’est une projection unique pour le territoire métropolitain.
Le tableau suivant donne les caractéristiques de cette nouvelle projection comparées à celles du Lambert II étendu de la NTF.
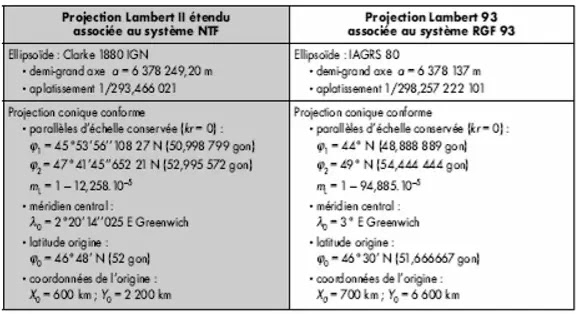

À partir des études basées sur les 1 000 sites du RBF, l’IGN calcule pour toute la France métropolitaine un modèle de paramètres de transformation passant du RGF 93 à la NTF et réciproquement, d’une précision décimétrique. Il est suffisant pour de nombreuses applications où une diffusion des coordonnées d’un chantier en système NTF est nécessaire, pour des raisons réglementaires ou contractuelles.
₪ Remarque
L’avantage principal d’un tel système est son universalité et son adéquation avec le système WGS 84 du gps triangulation.
Le principal inconvénient est que, du point de vue de la pratique quotidienne de la topométrie, les altérations linéaires qu’il induit sont trop importantes : près de 3 cm 10 m à Dunkerque, 1,5 cm pour 10 m à Perpignan et – 1 cm pour 10 m au voisinage de l’isomètre centrale 46° 30’. Pour mieux comprendre les problèmes que cela pose aux géomètres, reportez-vous à l’article
« incontournable géodésie » d’André Fontaine dans la revue XYZ n° 79 de juin 99.
₪ 2. ÉTABLISSEMENT DES CANEVAS PLANIMÉTRIQUES
La densité du canevas géodésique (environ un point pour 10 km2) est insuffisante pour rattacher les travaux topographiques nécessaires à la réalisation d’autoroutes, de tunnels, du TGV, au cadastre, au remembrement etc. d’une part ; d’autre part il se peut que pour certains travaux, la précision du canevas géodésique soit insuffisante.
Le topomètre est alors amené à asseoir le réseau polygonal qu’il réalise sur des points d’appui judicieusement répartis qui forment le canevas d’ensemble, canevas réduit mais de précision homogène.
Selon la précision désirée, le réseau créé est donc rattaché au canevas géodésique ou indépendant.
₪ 2.1. Définition
Un canevas est un ensemble discret de points judicieusement répartis sur la surface à lever, dont les positions relatives sont déterminées avec une précision au moins égale à celle que l’opérateur attend du levé. Ces points servent d’appui au lever des détails, implantations, etc.
Le canevas s’exprime par les coordonnées de ces points dans un même système.
₪ 2.2. Principe de densification
En topométrie, le principe fondamental consiste à aller de l’ensemble aux détails.
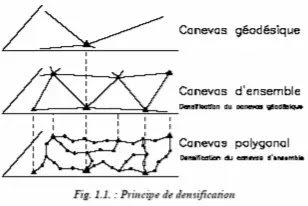

₪ 2.3. Canevas d’ensemble
Le canevas d’ensemble est un canevas planimétrique déterminé par des opérations de mesures sur le terrain, matérialisé de façon durable par des bornes ou des repères et suffisamment dense pour étayer le réseau sur lequel s’appuie le lever de détails.
Le canevas d’ensemble est en général appuyé sur le réseau géodésique ; on distingue :
❏ Le canevas d’ensemble ordinaire, dont la tolérance sur l’erreur en distance entre deux points est égale à 20 cm. Il est parfaitement adapté aux travaux en zones rurales. Pour les travaux cadastraux, le canevas d’ensemble est un canevas ordinaire. Il est donc rare, dans la pratique, de considérer un canevas de précision si ce n’est pour des travaux autres que cadastraux car un maître d’ouvrage peut avoir mis dans le cahier des charges un canevas de précision ;
❏ Le canevas d’ensemble de précision, dont la tolérance sur l’erreur en distance entre deux points est égale à 4 cm. Il est plutôt adapté aux travaux en zones urbaines et périurbaines.
Le canevas est indépendant si la précision du canevas géodésique d’appui est insuffisante, mais son orientation et son origine moyenne doivent être ramenées dans le système Lambert.
Ils doivent satisfaire à la gamme de tolérances fixées par l’arrêté du 21 janvier 1980.
₪ 2.3.1. Canevas ordinaire
Le canevas ordinaire est caractérisé par sa possibilité de densification par points isolés. Un tel point est déterminé par les mesures suivantes :
❏ Angulaires : intersection, relèvement, recoupement (procédés dits de triangulation) ;
❏ De distances : multilatération (procédé de trilatération) ;
❏ Mixtes : insertion.
Il peut également être :
❏ Un point nodal de cheminements à longs côtés.) ;
❏ Déterminé par localisation satellitaire.
₪ 2.3.1.1. La triangulation
La triangulation est une technique permettant de déterminer les éléments d’une figure en la décomposant en triangles adjacents dont l’opérateur mesure les angles au théodolite, dont il assure les fermetures angulaires et dont un côté au moins est connu ou déterminé. Elle peut avoir deux finalités, à savoir :
❏ Servir à densifier un réseau de triangulation déjà existant, par exemple le réseau géodésique : c’est le cas de canevas d’ensemble. Les mesures angulaires suffisent, mais il est possible d’améliorer la mise à l’échelle du réseau de triangulation en mesurant quelques bases ;
❏ Être locale : outre la mesure des angles, il faut alors effectuer impérativement la mesure de la longueur d’au moins une base du réseau de triangulation.
Par extension du premier type, on appelle triangulation complémentaire une densification du canevas par les procédés de l’intersection, du relèvement ou du recoupement, où l’opérateur mesure des angles sans assurer la fermeture des triangles.
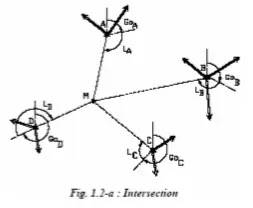
❏ Intersection Un point intersecté M est un point non stationné que l’opérateur vise depuis des points anciens connus en coordonnées A, B, C, D, encore appelés points d’appui, de manière à déterminer les gisements des visées d’intersection (fig. 1.2-a.). On ne pourra connaître précisément ces gisements que si on détermine les G0 des points d’appui. La figure 1.2-a. représente la réalisation d’une intersection. Toutes les lectures angulaires LA, LB, LC, et LD doivent être corrigées de la correction de réduction à la projection, dv.
Les gisements observés sont :
❏ GAM obs = Go A + LA
❏ GBM obs = Go B + LB
❏ GCM obs = Go C + LC
❏ GDM obs = Go D + LD
Les croquis sont représentés sur les « mappes d’observation » à très petite échelle (1/100 000 ou 1/200 000) par les désignations conventionnelles suivantes :
❏ Visée d’intersection désignée par une croix ;
❏ Points indiqués par leur numéro.
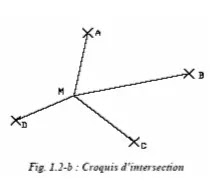
Le point M se situe sur chaque demi-droite matérialisant chaque visée : ces demi-droites sont les lieux géométriques de M ; il se situe donc à leur intersection. Dans ce procédé de l’intersection, on appelle lieux- droites du point M les demi–droites matérialisant les visées.
Deux lieux sont donc nécessaires et suffisants pour déterminer le point M ; en topographie, pour le contrôle, une visée supplémentaire est nécessaire et pour que le point M soit déterminé avec sécurité, il est conseillé d’effectuer une quatrième visée :
M est donc déterminé par quatre lieux, quel que soit le procédé utilisé.
Dans notre cas, quatre lieux droits seront nécessaires.
Les calculs d’une intersection sont détaillés au paragraphe 5
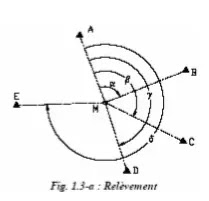
₪ Relèvement
Un point relevé est un point stationné depuis lequel l’opérateur effectue un tour d’horizon sur des points anciens connus (fig. 1.3-a.). L’opérateur lit les angles suivants :
❏ AMB = α= LB – LA
❏ AMC = β= LC – LA
❏ AMD = γ = LD – LA
❏ AME = δ = LE – LA
Sur les mappes d’observation, une visée de relèvement est représentée par un cercle (Fig. 1.3-b.).
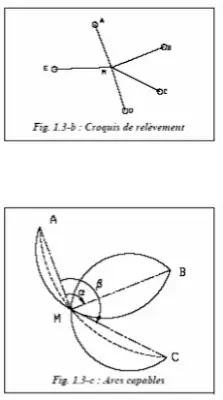
L’opérateur voit l’arc AB sous un angle α ; le point M se situe donc sur un arc de cercle passant par A, M et B : il est appelé arc capable AMB ; c’est un lieu géométrique du point M. Deux arcs capables sont donc nécessaires et suffisants pour déterminer par leur intersection le point M. Mais on sait qu’en topographie quatre lieux sont nécessaires pour le contrôle et la sécurité. Il faut donc quatre arcs capables.
Deux points donnent un arc capable d’angle associé α.
Trois points donnent trois arcs capables d’angles associés β et (β - α). Mais l’arc AMC, par exemple, passe forcément par l’intersection de AMB et BMC : on dit qu’il est dépendant. Donc trois points donnent seulement deux arcs capables indépendants. On dit que M est un point triple.
Il faut donc cinq points pour obtenir quatre arcs capables indépendants c’est-à-dire les quatre lieux indépendants nécessaires.
Le tableau suivant donne le nombre de lieux indépendants possibles et le nombre de points triples en fonction du nombre de points d’appui.
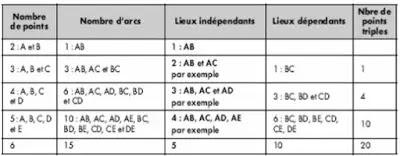

Le nombre d’arcs est une combinaison de n éléments pris deux à deux soit
❙ Cn2 = n (n-1) /2 ❙
Le nombre de points triples, intersections de trois arcs capables, est une combinaison de n points pris trois à trois, c’est à dire :
❙ C3n = n (n-1) (n-2) /6 ❙
₪ Recoupement
Le recoupement est le procédé qui utilise simultanément l’intersection et le relèvement pour la détermination d’un point.
Le point M de la figure 1.4. Est déterminé par recoupement à partir de trois visées d’intersection et trois visées de relèvement.
❏ Pour obtenir les quatre lieux nécessaires, il faut au minimum soit :
❏ Une visée d’intersection et quatre de relèvement soit 1 + 3 = 4 lieux indépendants
❏ Deux visées d’intersection et trois de relèvement soit 2 + 2 = 4 lieux indépendants ;
❏ Trois visées d’intersection et deux de relèvement soit 3 + 1 = 4 lieux indépendants.
Le recoupement est pratique quand les points d’appui sont peu nombreux et stationnables.
₪ 2.3.1.2. Trilatération
Le procédé utilisé est la multilatération. On observe les distances sur au moins quatre points éloignés correctement répartis ; les distances doivent être homogènes et les points situés dans les quatre quadrants, si possible autour du point nouveau à déterminer (point M, fig. 1.5-a.).
Le point M de la figure 1.5-b. est déterminé à partir de quatre mesures de distance DAMobs, DBMobs, DCMobs, DDMobs sur quatre points anciens connus.
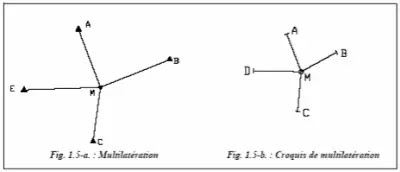

Les distances doivent être réduites au plan de projection.
Les lieux sont ici des cercles centrés sur les points connus et dont les rayons sont les distances mesurées réduites. Deux cercles sont nécessaires et suffisants pour déterminer le point M, mais il faut quatre lieux, donc quatre cercles, c’est-à-dire quatre points anciens connus.
Les distances mesurées sont indiquées par un trait perpendiculaire à la visée.
₪ 2.3.1.3. Insertion
L’insertion est un procédé qui utilise l’intersection, le relèvement et la multilatération pour la détermination d’un point.
On note :
❏ I une visée d’intersection ;
❏ R une visée de relèvement ;
❏ M une visée de multilatération.
Les combinaisons suivantes permettent d’obtenir les quatres lieux nécessaires :
❏ 1 x I + 3 x R + 1 x M = 1 + 2 + 1 = 4 lieux
❏ 1 x I + 2 x R + 2 x M = 1 + 1 + 2 = 4 lieux
❏ 2 x I + 2 x R + 1 x M = 2 + 1 + 1 = 4 lieux
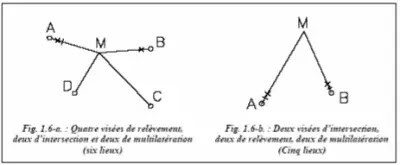
Ces combinaisons ne sont données qu’à titre d’exemples, car il paraît évident que si une mesure de distance est possible sur un nouveau point, une visée d’intersection l’est aussi ; donc il y a autant de visées d’intersection que de multilatérations.
L’insertion présente l’intérêt d’être opérationnelle avec un petit nombre de points d’appui stationnables.
₪ 2.3.1.4. Point nodal, intersection d.au moins trois cheminements à longs côtés
Cette méthode permet de remplacer les méthodes précédentes quand la nature du terrain interdit la réalisation d’un réseau de triangles.
Seuls les points nodaux, définis comme les points de rencontre d’au moins trois cheminements à longs côtés, remplacent les points du canevas que l’on aurait déterminés par triangulation ou trilatération.
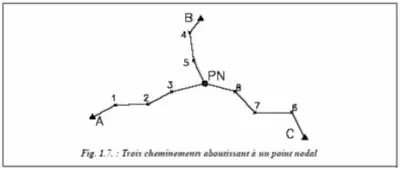
Les points A, B et C de (fig. 1.7.) sont connus et stationnables. PN est le point nodal.
1, 2, 3, etc. sont des points intermédiaires. Les côtés des cheminements ont une longueur de 500 m sans être inférieurs à 200 m.
₪ 2.3.1.5. Canevas établi par localisation satellitaire (réseau GPS)
La densification du canevas géodésique s’effectue de plus en plus par GPS, surtout depuis que le nouveau Réseau Géodésique Français (RGF,) commence à être diffusé par l’IGN.
₪ 2.3.2. Opérations annexes de « rattachement »
Les procédés classiques de détermination de points de canevas sont subordonnés à l’inter visibilité, contrairement au GPS, et il est rare que l’opérateur puisse tout observer d’un ou sur un point à cause de la présence de masques : arbres, immeubles, relief, etc. d’où la nécessité de s’excentrer par rapport au point de station.
D’une manière générale, en dehors des procédés étudiés précédemment, la détermination d’un point nouveau du canevas d’ensemble par rapport à un ou plusieurs autres s’appelle rattachement.
₪ 2.3.2.1. Rattachement simple
Le rattachement simple est une opération annexe du canevas d’ensemble qui consiste à déterminer, au voisinage d’un repère A connu en coordonnées rectangulaires, les coordonnées d’un point M qui présente de plus grandes facilités d’utilisation ou de meilleures chances de conservation. Cette opération s’effectue généralement par rayonnement planimétrique.
Par exemple, B et C (fig. 1.8.) sont des points éloignés connus. L’opérateur stationne le point A connu où l’on détermine un G0 de station.
Si LM est la lecture sur le point M, on peut écrire :
❙ GAM = G0 + LM. ❙
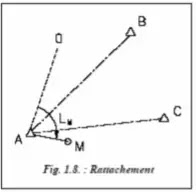
La lecture de LM au mgon suffit puisque la distance LM ne dépasse pas 100 m ; or 1 mgon correspondent à un déplacement de 1,57 mm à l’extrémité d’une visée de 100 m.
Puis on mesure la distance AM :
DhAM. On en déduit : EM = EA + DhAM. SinGAM NM = NA + DhAM. CosGAM
En général, pour plus de sûreté, on double la mesure des observations (angle et distance). Par exemple, dans le cas d’un tour d’horizon au point A, on effectue la lecture sur le point M à la fin de deux séquences.
On peut rencontrer ce cas lors du relèvement d’un point nouveau P ; le point connu A n’est pas visible mais un point M à proximité muni d’une balise est visible de P.
₪ 2.3.3. Méthodes opératoires pour l’établissement du canevas
₪ 2.3.3.1. Techniques préparatoires
❏ Étude d’un projet à l’aide de cartes et de photographies aériennes
Pour l’exécution de la mission qui lui est confiée, le géomètre dispose des éléments suivants :
❏ Une copie de l’arrêté d’ouverture des travaux ;
❏ Une carte au 1/50 000 ;
❏ Une carte au 1/25 000 ;
❏ Une liste des coordonnées des points géodésiques et des sommets des triangulations cadastrales susceptibles d’être utilisés comme points d’appui, accompagnée de leur fiche signalétique.
Sur cartes, après avoir défini le périmètre des opérations, le géomètre trace les lignes caractéristiques du terrain : lignes de crêtes en rouge, lignes de talwegs en bleu ; puis il choisit sur la carte l’emplacement des points du CEO (canevas d’ensemble ordinaire) en respectant la densité imposée :
❏ Le CEO étant plutôt adapté aux zones rurales, la densité est généralement d’environ un point par km2 ou un point pour 100 ha ;
❏ Le CEP étant plutôt adapté aux zones urbaines ou périurbaines, il est préconisé deux à quatre points par km2 en zone urbaine et environ deux points par km2 en zone périurbaine.
Le choix est effectué aussi en fonction des différentes techniques possibles que sont les procédés de triangulation et de trilatération, l’insertion et les cheminements à longs côtés : dans une zone de plaine, on adopte plutôt les cheminements à longs côtés pour déterminer les points nodaux qui sont les points du canevas ; en revanche, dans une zone plus vallonnée, la triangulation et la trilatération sont des méthodes plus efficaces.
Puis le géomètre établit la mappe des observations :
❏ En traçant les cheminements dans le premier cas ;
❏ En schématisant les visées avec leur symbole dans le second cas.
Ils peuvent être aussi des repères fixés sur des terrasses de bâtiment, des antennes, des clochers, des sommets de pylônes, etc.
Ils sont numérotés et repérés par trois ou quatre repères auxiliaires à l’aide de croquis cotés permettant le rétablissement des points détruits sans observations nouvelles.
❏ Numérotation des points du canevas
Chaque géomètre a sa propre façon de numéroter les stations de canevas ; le cahier des charges peut néanmoins imposer la numérotation.

❏ Fiches signalétiques des sommets
L’opérateur établit pour tous les sommets une fiche signalétique, qui comprend :
❏ L d’une part des renseignements concernant la nature du point, le propriétaire de l’îlot de propriété où est implantée la borne et les références cadastrales ;
❏ Les coordonnées du point et la zone Lambert de rattachement ;
❏ D’autre part, trois croquis :
♦ Le croquis de situation, qui a pour objet de permettre à toute personne n’ayant pas participé aux travaux de retrouver rapidement l’emplacement approximatif de la borne à partir d’un détail caractéristique du terrain ou de la carte : donnez au moins rois cotes par rapport à des points durs facilement repérables ;
♦ Le croquis visuel est une vue perspective schématique du point ;
♦ Le croquis de repérage, qui permet de retrouver le repère souterrain d’une borne disparue et de la réimplanter à sa position exacte. Ce croquis n’est établi que s’il existe dans un rayon d’une cinquantaine de mètres des détails fixes et durables.
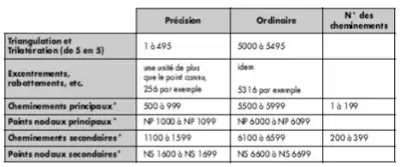
Pour un chantier donné, aucun numéro identique ne doit apparaître pour plusieurs sommets. Ils doivent tous être distincts selon la nature du canevas à laquelle ils appartiennent ; le tableau ci-après donne un exemple de numérotation :
Les cotes figurant sur ce croquis doivent être relevées avec précision et pouvoir être appliquées sur le terrain malgré la disparition éventuelle de la borne.
La fiche signalétique suivante est issue de la triangulation complémentaire de Biot (06).


₪ 2.3.3.2. Mesure sur le terrain
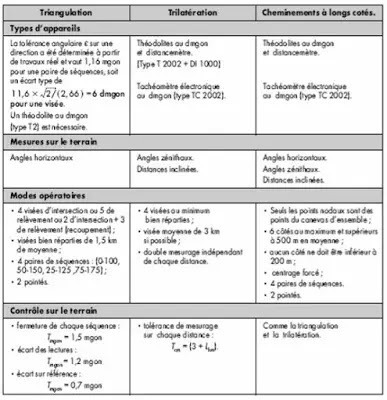
Il convient de choisir le matériel et la méthodologie adéquats pour respecter les tolérances légales imposées. En canevas ordinaire, on préconise les recommandations du tableau suivant :
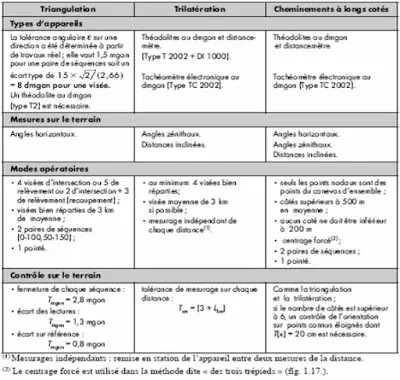

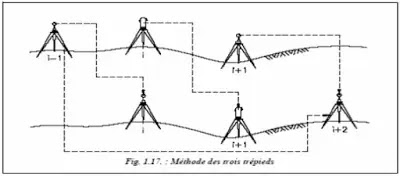
La méthode des trois trépieds cités dans le tableau précédent, est mise en œuvre comme suit :
❏ Le théodolite est en station i (fig. 1.17.), les voyants aux sommets i–1 et i+1 sont placés dans des embases à centrage forcé ; on mesure l’angle au sommet i ;
❏ Le voyant i–1 vient dans l’embase du théodolite en i, le trépied et son embase en i–1 sont mis en station au sommet i+2 et le voyant i+1 y est placé ;
❏ Le théodolite va dans l’embase i+1, on mesure l’angle au sommet i+1, etc.
Les erreurs de centrage sont ainsi réduites au minimum.

L’utilisation du centrage forcé se justifie ainsi :


L’arrêté ministériel du 20 Janvier 1980 impose une tolérance sur un angle du cheminement de 1,4 mgon, soit 1 mgon sur une direction aussi bien en canevas ordinaire que de précision ; l’écart type correspondant est 1 mgon / 2,66 ≈ 0,4 mgon.
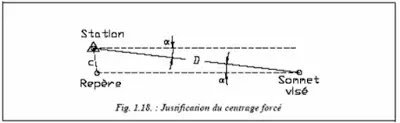
Pour une visée de l’ordre de 500 m, la précision de centrage c (fig. 1.18.) doit être de :
c = 1,57 x 0,500 x 0,4 ≈ 3 mm (en utilisant la sensibilité, Le centrage doit être réalisé avec une précision de 3 / √mm, soit 2 mm environ en considérant que les écarts de centrage de
L’appareil c1 et du réflecteur c2 sont égaux à C = C²1 + C²2 Cette précision est difficile à obtenir sans centrage forcé.

En canevas de précision, il est préconisé :

Tenue des carnets d’observations
La saisie des données est la phase la plus importante ; les carnets d’observation doivent être facilement exploitables.
À cet effet, ils doivent présenter :
❏ La date et l’heure,
❏ Le nom de l’opérateur,
❏ Le numéro du carnet,
₪ 3. LA MULTILATÉRATION
Nous commençons par cette méthode car elle nous paraît la plus simple en termes de compréhension et de calculs.
₪ 3.1. Coordonnées approchées par bilatération
Les distances sur deux points anciens connus sont suffisantes pour calculer un point approché Mo : on appelle ces deux mesures bilatération.
Considérons un point Mo dont on veut déterminer les coordonnées à partir de A et B (par convention A, B, Mo sont pris dans le sens horaire). On mesure les distances DAMo et DBMo puis on calcule les coordonnées du point Mo comme suit :
Calcul de l'angle
❚ Cos = D² AM0 + D² AB – D BM0 / 2DAB.DAM0 ❚
Calcul du gisement GAMo:
Si le point Mo est à droite du vecteur AB, on peut écrire : GAMo = GAB + α.
Si le point Mo est à gauche du vecteur AB, on peut écrire : GAMo = GAB – α.
Les coordonnées du point Mo sont alors :
EMo = EA + DAMo. SinGAMo
NMo = NA + DAMo. CosGAMo
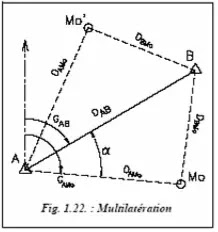
Attention : il existe deux points possibles Mo et Mo’ ; il faut en choisir un, par exemple à partir d’un schéma à l’échelle. Ces calculs ramènent à une intersection de deux cercles.
Pour vérifier, on effectue les mêmes calculs de rayonnement à partir du point B.
₪ 4. L. INTERSECTION
Comme la multilatération, cette deuxième méthode est relativement simple à comprendre. Mais en termes de manipulation sur le terrain, elle nécessite plus de travail car chaque point d’appui est stationné et à chaque station un G0moyen de station est calculé.
Les principes déjà développés dans la multilatération ne seront pas repris dans le détail.
₪ 4.1. Détermination d’un point approché à partir de deux visées
On détermine les coordonnées d’un point approché Mo à partir de deux visées d’intersection correctement choisies (lectures précises, visées longues, se coupant sous un angle favorable, c’est-à-dire proche de 100 gon).
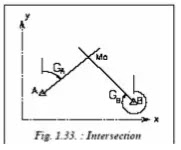
Les deux points choisis sont nommés A et B (fig. 1.33.).
Les formules de Delambre donnent :
YM0 = YA+ (XA - XB) - (YA -YB). tanGB /tanGB – tanGA
XM0 = XA + (YM0 – YA). TanGA
Les gisements GA et GB sont connus à 200 gon près.
₪ 5. LE RELÈVEMENT
Plus complexe que les deux méthodes précédentes, le relèvement reste plus simple à réaliser sur le terrain puisqu’il ne nécessite qu’une seule station. La précision des visées angulaires étant meilleure pour des visées lointaines, c’est la méthode idéale pour de longues visées sans possibilité de mesure de distance.
₪ 5.1. Coordonnées approchées à partir de trois visées
On détermine les coordonnées d’un point approché Mo à partir de trois visées de relèvement correctement choisies : elles doivent être longues et bien réparties autour du point cherché M et doivent se couper sous un angle favorable (proche de 100 gon) mais en évitant les couples de visées parallèles.
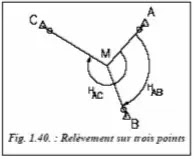
Les coordonnées du point approché Mo sont calculées à partir des formules de Delambre pour le relèvement, c’est-à-dire :
TanGAM = (XB–XA). CotanHAB– (XC–XA). CotanHAC + (YC–YB) / (YB-YA). CotanHAB- (YC-YA). CotanHAC-(XC-XB);
TanGBM = tan (GAM + HAB) = tanGAM + tanHAB/1 - tanGAM.tanHAB
On reporté ensuite ces résultats dans les formules de Delambre utilisées pour l’intersection.
















Aucun commentaire:
Enregistrer un commentaire